Variance Calculator: The Spread of a Sample or Population

Variance is a measure of dispersion that evaluates how far each number in a data set is from its average. To calculate the mean, add each observation in the dataset together, then divide the result by the sample size (or population size). Use the variance calculator to compute both sample variance and population variance, complete with a step-by-step solution, and then present the results in APA format.

Statistics Calculator: Variance

It shows the distribution of the random variable by the mean value. This variance finder will give you the number of samples, mean, standard flat tax impact on saving and the economy deviation, and variance in one click. Using this calculator, you will get step-by-step results of standard deviation, mean, and variance.

Sample Bias

It can be disproportionately influenced by outliers, which significantly impact the sum of all the squared differences together. Additionally, variance does not indicate the direction of data spread and can be less intuitive due to the squaring of all the squared differences together. Calculating variance is crucial in data analysis as it quantifies the degree of variation or dispersion within a data or set of data values. A high variance indicates a wider spread of data values, while a low variance suggests closer clustering around the mean. Understanding variance is key in various fields for informed decision-making. Our Variance Calculator analyzes discrete data sets to compute mean, variance, and standard deviation, also displaying the calculation process.

Variance Calculator with steps

It simplifies the process to calculate variance, by automating the computation of squared differences between each data point and the mean. Users input a series of data values, and the variance calculator provides the variance, indicating the degree of spread in the data set. This tool is particularly useful in data analysis, saving time and reducing errors that can occur in manual calculations.

In statistics, the term variance refers to a statistical measurement of the spread between numbers in a data set from the mean. To calculate the population variance, you need the entire dataset. Follow these steps to measure the variance for the given data set using this formula. Variance calculator is an online free tool to calculate the variation of each number in a data set from the mean value of that data set.

• The variance is equal to the sum of squares SS divided by the sample size n minus 1.
• The variance is the mean of the square of the distance from each point to the mean.
• If you have many outcomes that all come from the same probability distribution, for example, men’s heights, then that entire set of data has a mean and variance.
• The variance of a group or set of numbers is a number that represents the ‘spread’ of the set.
• The calculator also outputs the standard deviation, mean, range, count, and SEM.
• The formula for each is the square root of their respective variances, aligning the values of the units of measure with those of the data.

Specify whether the total number of data points represent a sample population or the entire population. This choice will determine the variance formula used in the calculation. Given a discrete data set representing a sample or a population, the calculator calculates the mean, variance, and standard deviation and displays the workflow involved in the calculation.

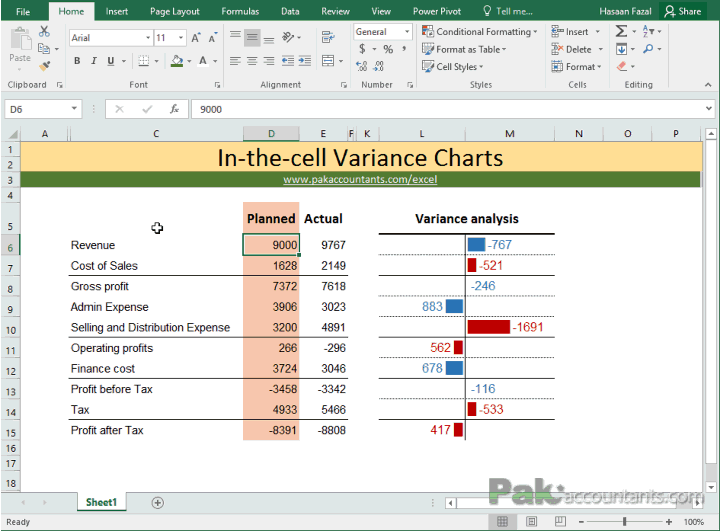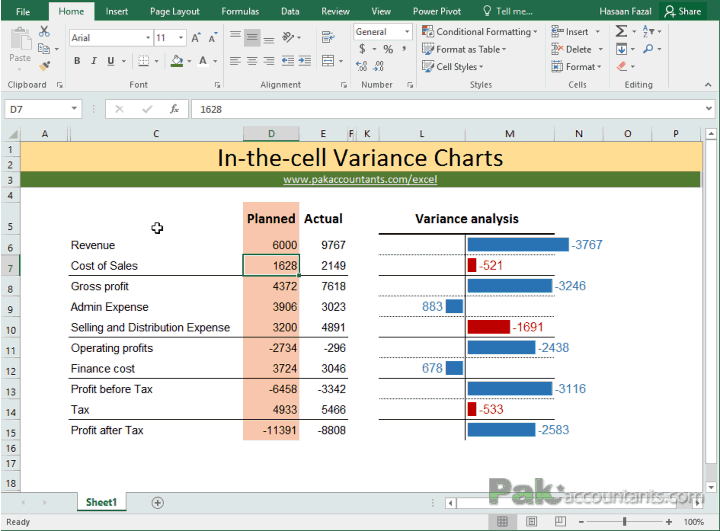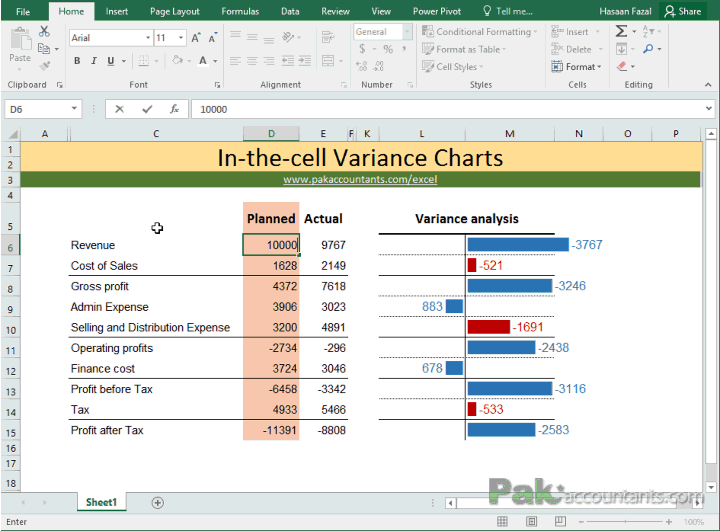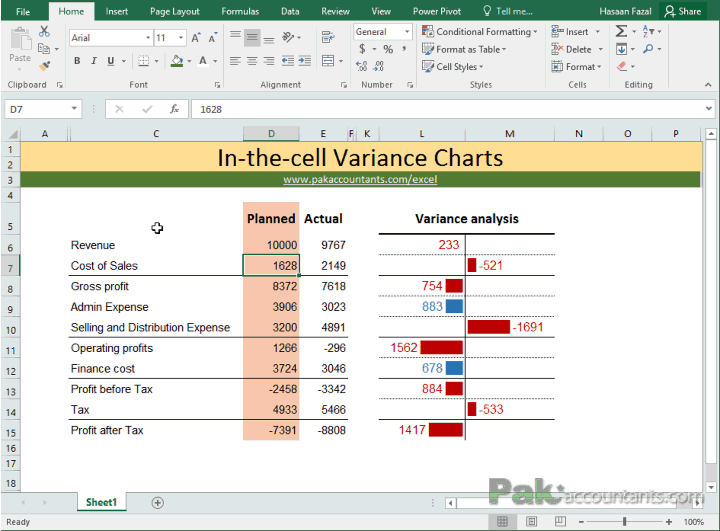
The variance for a population is equal to the sum of squares divided by the size of the population. When working with a sample, the population variance is a biased estimator of the variance in the underlying distribution. For an unbiased statistic, we expect to get a standard deviation of 4 and a variance of 16.You may notice that dividing by (n-1) yields better results than dividing by n. The result for the variance is not biased; it is very close to 16, while the result for the standard deviation is biased.

It is calculated as the average of squared differences, and since squares are always non-negative, the average resulting variance is also non-negative. A variance of zero indicates identical data values across the same set of data. This data value can include any series of numerical data value, values from your sample data set or entire population data only. When you do not have data for the entire population, you calculate the sample variance from the sampled data.

Which one is appropriate depends on whether one wants to estimate the variance based on a sample from a population or to find the variance of a whole population that can be directly observed. Learning how to calculate variance is a key step in computing standard deviation. These two measures are the foundation to calculating relative standard deviation and confidence intervals. In the table below, the squared deviation calculated from the mean of all test results. The “Mean Deviation” column is the score minus 30, and the “Standard Deviation” column is the column before the square.